NDCG评估指标
NDCG用于评估搜索返回的结果相关性指标。其由CG转换到DCG再发展出nDCG。下面依次介绍。
累计增益(CG)
CG,cumulative gain,是DCG的前身,只考虑到了相关性的关联程度,没有考虑到位置的因素。它是一个搜素结果相关性分数的总和。指定位置P上的CG为:
其中$rel_i$为第$i$个位置上的文档和query的相关性。
该度量方法存在问题,因为其无法区分排序顺序,只能判断召回的数据是否相关,比如一个query应该召回三个文档$a,b,c$。其相关性依次降低,但如果召回的实际顺序是$c,b,a$时,该评估指标和最优情况下的指标值是一样的。
为解决上述问题,引入了DCG。
折损累计增益(DCG)
相比于CG,DCG在CG的每一个结果上增加了一个折损值。目的就是为了让排名越靠前的结果越能影响最后的结果。假设排序越往后,价值越低。到第i个位置的时候,它的价值是 $\frac{1}{log_2{(i+1)}}$,那么第i个结果产生的效益就是 $rel_i * \frac{1}{log_2{(i+1)}}$,因此:
因为是乘以一个折损值,因此该值可以取别的函数,还有一个更加常用的公式,如下:
DCG解决了同一个query下排序的指标,但是对于不同query其召回的文档数量是不一致的,DCG采用的是累加的方式,这对应召回文档更多的query是更加友好的,但不符合实际使用,因此NDCG被提出以改进DCG。
归一化折损累计增益(NDCG)
由于DCG是一个累加值,无法对不同搜索结果进行比较,因此NDCC对每个query的结果进行了归一化操作,其方法是对DCG值除以IDCG(理想情况下最大DCG值):
其中$\vert REL \vert$表示,结果按照相关性从大到小的顺序排序,取前P个结构组合成的集合,即按照最优的方式对结果进行排序是的DCG值。
排序学习LTR
排序学习(Learning to Rank,LTR),也称机器排序学习(Machine-learned Ranking,MLR) ,就是使用机器学习的技术解决排序问题。
传统的检索模型所考虑的因素并不多,主要是利用词频、逆文档频率和文档长度、文档重要度这几个因子来人工拟合排序公式,且其中大多数模型都包含参数,也就需要通过不断的实验确定最佳的参数组合,以此来形成相关性打分。
LTR 则是基于特征,通过机器学习算法训练来学习到最佳的拟合公式,相比传统的排序方法。
排序学习的模型通常分为单点法(Pointwise Approach)、配对法(Pairwise Approach)和列表法(Listwise Approach)三大类,三种方法并不是特定的算法,而是排序学习模型的设计思路,主要区别体现在损失函数(Loss Function)、以及相应的标签标注方式和优化方法的不同。
单点法
单点法排序学习模型的每一个训练样本都仅仅是某一个查询关键字和某一个文档的配对。它们之间是否相关,与其他文档和其他查询关键字都没有关系。
配对法
配对法的基本思路是对样本进行两两比较,构建偏序文档对,从比较中学习排序,因为对于一个查询关键字来说,最重要的其实不是针对某一个文档的相关性是否估计得准确,而是要能够正确估计一组文档之间的 “相对关系”。
列表法
相对于尝试学习每一个样本是否相关或者两个文档的相对比较关系,列表法排序学习的基本思路是尝试直接优化像 NDCG(Normalized Discounted Cumulative Gain)这样的指标,从而能够学习到最佳排序结果。
LambdaMART算法
LambdaMART 的提出先后经由 RankNet、LambdaRank 逐步演化而来。
RankNet
RankNet 的核心是提出了一种概率损失函数来学习 Ranking Function,并应用 Ranking Function 对文档进行排序。
RankNet网络将输入query的特征向量$x\in R^n$,映射为一个实数$f(x) \in R$。具体的,给定两个query下的两个文档$U_i$和$U_j$,其特征值分别为$x_i$,$x_j$,经过RankNet进行前向计算得到相应的对应分数$s_i = f(x_i) $,$s_j=f(x_j)$。使用$U_i \triangleright U_j$表示$U_i$比$U_j$排序更靠前(如对某个 query 来说,𝑈𝑖 被标记为 “good”,𝑈𝑗 被标记为 “bad”)。RankNet把排序问题转化成比较一个$(U_i,U_j)$文档对的排序问题,首先计算每个文档得分,定义使用下面的公式计算根据模型得分获取的$U_i$比$U_j$排序更靠前的概率:
这个概率就是深度学习中常用的sigmoid函数,由于参数$\sigma$只影响函数形状,对最终结果影响不大,因此通常使用$\sigma=1$进行简化。
可以看到RankNet预测的分数$s_i>s_j$且差距越大时,$P_{ij}$越接近1,即$U_i$排序就应该在$U_j$前概率越大,反之则$U_j$在$U_i$之前概率越大。
RankNet 证明了如果知道一个待排序文档的排列中相邻两个文档之间的排序概率,则通过推导可以算出每两个文档之间的排序概率。因此对于一个待排序文档序列,只需计算相邻文档之间的排序概率,不需要计算所有 pair,减少计算量。
真实的相关性概率
对于特定query,定义$S_{ij} \in {0,\pm 1}$为文档$U_i$和文档$U_j$被标记的标签之间的关联,即:
因此可以定义文档$U_i$比文档$U_j$更相关的真实概率为:
损失函数
对于一个排序,RankNet 从各个 doc 的相对关系来评价排序结果的好坏,排序的效果越好,那么有错误相对关系的 pair 就越少。所谓错误的相对关系即如果根据模型输出 𝑈𝑖 排在 𝑈𝑗 前面,但真实 label 为 𝑈𝑖 的相关性小于 𝑈𝑗,那么就记一个错误 pair,RankNet 本质上就是以错误的 pair 最少为优化目标,也就是说 RankNet 的目的是优化逆序对数。而在抽象成损失函数时,RankNet 实际上是引入了概率的思想:不是直接判断 𝑈𝑖 排在 𝑈𝑗 前面,而是说 𝑈𝑖 以一定的概率 P 排在 𝑈𝑗 前面,即是以预测概率与真实概率的差距最小作为优化目标。最后,RankNet 使用交叉熵(Cross Entropy)作为损失函数,来衡量 $P_{ij}$ 对 $\overline{P_{ij}}$ 的拟合程度:
化简后:
当$S_{ij}=1$时:
当$S_{ij}=-1$时:
从损失函数可以看出,如果对文档$U_i$和$U_j$的打分可以正确拟合标签时,则$L_{ij}$趋于0,否则趋于线性函数。具体的,假如$S_{ij}$=1,则$U_i$应该比$U_j$排序高:
如果$s_i > s_j$则拟合的分数可以正确排序文档:
如果$s_i<s_j$,则拟合的分数不能正确排序文档:
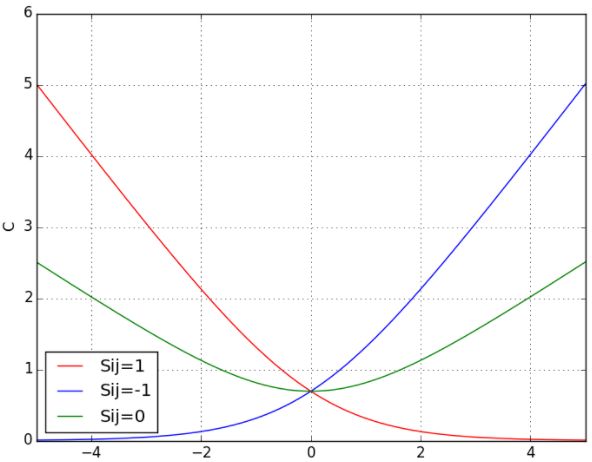
下图展示了当$S_{ij}$分别取1,0,-1时,损失函数以$s_i-s_j$为变量的取值示意图:
该损失函数具有如下特点:
- 当两个相关性不同的文档算出来的模型分数相同时,即 𝑠𝑖=𝑠𝑗,此时的损失函数的值为 log2,依然大于 0,仍会对这对 pair 做惩罚,使他们的排序位置区分开。
- 损失函数是一个类线性函数,可以有效减少异常样本数据对模型的影响,因此具有鲁棒性。
Ranknet 最终目标是训练出一个打分函数$s=f(x,w)$,使得所有 pair 的排序概率估计的损失最小,即:
其中,𝐼 表示所有在同一 query 下,且具有不同相关性判断的 doc pair,每个 pair 有且仅有一次。
通常该打分函数只要光滑可导即可。
参数更新
RankNet 采用神经网络模型优化损失函数,也就是后向传播过程,采用梯度下降法求解并更新参数:
其中$\eta$为学习率。RankNet 是一种方法框架,因此这里的 𝑤𝑘 可以是 NN、LR、GBDT 等算法的权重。
对RankNet的梯度$\frac{\partial L} {\partial w_k}$进行因式分解,有:
其中:
$s_i$和$s_j$对$w_k$的偏导数可以根据实际使用的模型求的。
结果排序最终由模型得分$s_i$确定,其梯度很关键,定义:
对于有序对$(i,j)$,有$S_{ij}= 1$,于是化简:
此时$\lambda_{ij}$始终为负数,使用梯度更新时,将会使$s_i$增大,因此,对于文档$U_i$来说,真实的相关性在其后的文档将促进其分数增加。即给其一个向上推的力。
由于:
对于$s_j$来说,其导数均为正数,则在更新模型时使$s_j$变小,因此对应任意文档来说,真实的相关性在其前的文档都将促使其分数减小,即给其一个向下推的力。
这个$lambda_{ij}$即为接下来介绍的LambdaRank 和 LambdaMART 中的 Lambda,称为 Lambda 梯度。
LambdaRank
RankNet 本质上就是以错误的 pair 最少为优化目标,也就是说 RankNet 的直接目的就是优化逆序对数(pairwise error),这种方式一定程度上能够解决一些排序问题,但它并不完美。
逆序对数(pairwise error)表示一个排列中,抽查任意两个 item,一共有 $C_2^n$ 种可能的组合,如果这两个 item 的之间的相对排序错误,逆序对数量增加 1。
逆序对数的实质就是插入排序过程中要移动元素的次数。直观理解为要想把某个元素移动到最优排序位置,需要移动多少次,两个元素就是二者移动次数的和。
例如,对某个 Query,和它相关的文章有两个,记为 (𝑄,[𝐷1,𝐷2]) 。
- 如果模型 𝑓(⋅) 对此 Query 返回的 n 条结果中, 𝐷1,𝐷2 分别位于前两位,那么 pairwise error 就为 0;
- 如果模型 𝑓(⋅) 对此 Query 返回的 n 条结果中, 𝐷1,𝐷2 分别位于第 1 位和第 n 位,那么 pairwise error 为 n-2;
- 如果模型 𝑓(⋅) 对此 Query 返回的 n 条结果中, 𝐷1,𝐷2 分别位于第 2 和第 3 位,那么 pair-wise error 为 2;
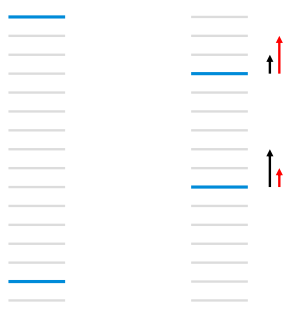
假设RankNet经过两轮迭代实现下图所示的顺序优化:
第一轮的时候逆序对数为 13,第二轮为 3 + 8 = 11,逆序对数从 13 优化到 11,损失确实是减小了,如果用 AUC 作为评价指标,也可以获得指标的提升。但实际上,我们不难发现,优化逆序对数并没有考虑位置的权重,这与我们实际希望的排序目标不一致。下一轮迭代,RankNet 为了获得更大的逆序对数的减小,会按照黑色箭头那样的趋势,排名靠前的文档优化力度会减弱,更多的重心是把后一个文档往前排,这与我们搜索排序目标是不一致的,我们更希望出现红色箭头的趋势,优化的重点放在排名靠前的文档,尽可能地先让它排在最优位置。所以我们需要一个能够考虑位置权重的优化指标。
RankNet 以优化逆序对数为目标,并没有考虑位置的权重,这种优化方式对 AUC 这类评价指标比较友好,但实际的排序结果与现实的排序需求不一致,现实中的排序需求更加注重头部的相关度,排序评价指标选用 NDCG 这一类的指标才更加符合实际需求。而 RankNet 这种以优化逆序对数为目的的交叉熵损失,并不能直接或者间接优化 NDCG 这样的指标。
对于绝大多数的优化过程来说,目标函数很多时候仅仅是为了推导梯度而存在的。而如果我们直接就得到了梯度,那自然就不需要目标函数了。
微软学者经过分析,就直接把 RankNet 最后得到的 Lambda 梯度拿来作为 LambdaRank 的梯度来用了,这也是 LambdaRank 中 Lambda 的含义。这样我们便知道了 LambdaRank 其实是一个经验算法,它不是通过显示定义损失函数再求梯度的方式对排序问题进行求解,而是分析排序问题需要的梯度的物理意义,直接定义梯度,即 Lambda 梯度。有了梯度,就不用关心损失函数是否连续、是否可微了,所以,微软学者直接把 NDCG 这个更完善的评价指标与 Lambda 梯度结合了起来,就形成了 LambdaRank。
首先来分析一下lambda梯度的意义:LambdaRank 中的 Lambd 其实就是 RankNet 中的梯度 $\lambda_{ij}$, $\lambda_{ij}$可以看成是 𝑈𝑖 和 𝑈𝑗 中间的作用力,代表下一次迭代优化的方向和强度。如果 𝑈𝑖⊳𝑈𝑗,则 𝑈𝑗 会给予 𝑈𝑖 向上的大小为 $\lambda_{ij}$ 的推动力,而对应地 𝑈𝑖 会给予 𝑈𝑗 向下的大小为 $\lambda_{ij}$ 的推动力。对应上面的那张图,Lambda 的物理意义可以理解为图中箭头,即优化趋势。
因此,直接使用$\vert \triangle_{NDCG} \vert $乘以$\lambda_{ij}$,就可以得到LambdaRank的Lambda,即:
其中$\vert \triangle_{NDCG} \vert $为$U_i$和$U_j$交换排序位置得到的NDCG差值的绝对值。通过前文的描述我们可以知道,NDCG指标考虑了排序位置的影响,$\vert \triangle_{NDCG} \vert $值为在全部召回队列中仅考虑i和j两个文档时,互换位置对最终DNCG分数的影响。
对于$U_i \rhd U_j$来说,如果返回的分数排序后$U_i$对应$index_1$,$U_j$对应$index_j$。则:
从上试我们可以得知,大两个文档的真实分数差越大时,结果的$\vert \triangle_{NDCG} \vert $值越大,这样就起到了对于排名高并且相关性高的文档更快地向上推动,而排名低而且相关性较低的文档较慢地向上推动。
对于特定$U_i$,累加其他所有排序项的影响,得到:
即,对于每个文档,分别计算与排在其后的所有文档的$\lambda_{ij}$和与排在其前的所有文档的$\lambda_{ki}$,对这些值进行求和。
从之前的分析我们知道,排在其后的文档给予当前文档一个向上推动的力,排在其后的文档给予其向下推动的力。因此为了保证相关性更高的文档排序更高(对相关性低的类似,让其排序更靠后),因此我们直接拟合$\lambda_i$即可。
如果将$\lambda_i$看做一个导数,那么我们可以推出其效用函数为:
LambdaMART算法
LambdaRank 重新定义了梯度,赋予了梯度新的物理意义,因此,所有可以使用梯度下降法求解的模型都可以使用这个梯度,基于决策树的 MART 就是其中一种,将梯度 Lambda 和 MART 结合就是大名鼎鼎的 LambdaMART。
MART即为GBDT,LambdaMART 只是在 GBDT 的过程中做了一个很小的修改。原始 GBDT 的原理是直接在函数空间对函数进行求解模型,结果由许多棵树组成,每棵树的拟合目标是损失函数的梯度,而在 LambdaMART 中这个梯度就换成了 Lambda 梯度,这样就使得 GBDT 并不是直接优化二分分类问题,而是一个改装了的二分分类问题,也就是在优化的时候优先考虑能够进一步改进 NDCG 的方向。
LambdaMART整体流程如下:
其执行逻辑如下:
隐含步骤:使用当前模型$F(x)$的输出$s$计算效用函数$C$。这里实际并不会执行,因为我们已经直接找到了其梯度,不需要通过效用函数来计算梯度。这里是提醒读者,每轮循环优化的目标,依然是最小化效用函数。
每棵树的训练都会先遍历所有的数据,计算每个pair(同一个query下的)互换位置导致的指标变化$\vert \triangle_{NDCG} \vert $以及lambda值,即:
之后计算每个文档的Lambda:
通过lambda梯度我们推出效用函数为:
由此可得:
定义:
则:
计算每个$ y_i$对$\lambda_i$的倒数,用于后续使用牛顿法求解叶子节点的数值:
使用$(X, \lambda)$,拟合一个决策回归树,作为本轮循环生成的弱分类器。注意,这里的$\lambda$是上一步的$-y_i$,即负梯度。
对第二步生成的回归树,计算每个叶子节点的数值,采用牛顿迭代法求解。
牛顿法是对于一个函数,使用泰勒展开,忽略高阶项的一个迭代优化方式。例如对于任意$f(X)$,在任意点$x_n$进行泰勒展示为:
牛顿法忽略高阶项,之后如果要使得函数$f(x)$最小,则找到$f(x)$梯度为0,即:
GBDT对的每个叶节点的计算为:
对应到lambdaMART算法,当前的$x_i$对应为输入$x_i$。函数$f_{t-1}(x)$对应于当前输出的$s_i$分数。$L$对应于效用函数$C$。这里$s_i$的实际是当前已经训练的弱模型的加和即:$s_i=F_{k-1}(x_i)$,其中$k$-1为当前训练的回归树数量。
利用牛顿法,获取最小化效用函数时输入为:
此时$s_i-s_j = f_{t-1}(x_i)$,因此:
对应上图$\gamma_{lk}$的计算:
这里缺失一个负号,我理解是上图有错误,在使用回归树拟合的时候,拟合的是负梯度,即$y_i = -\lambda_i$,对于二阶导,应该使用原$\lambda$的二阶导,这样相除就存在一个负号,这样求出的$\gamma_{lk}$才是上图中的形式。
模型更新
使用牛顿法更新模型,将第k颗树增加到模型中。模型更新如下:
其中$\eta$为学习率。
程序执行逻辑
1 | def train(train_data, valid_data, model_save_path): |
读取数据
pyltr.data.letor.read_dataset逻辑:
1 | /* |
1 | # 参数与上述的函数一致 |
根据上述代码,可以直到,pyltr读取数据的格式如下:
1 | y weight qid:value x_1:value_1 x_2:value_2 ... x_n:value_n |
其中y和weight非必须(训练应该必须有y)qid的value用于划分pair,x_i为输入的x向量,如果某个向量没有,可以不在文件中存在,使用missing填充。comment是这条数据对应的额外信息,如query和对应的doc。
注意qid必须要是同一个的连续存放。
lambdaMart
初始化参数
| 参数 | 类型 | 含义 | 默认值 |
|---|---|---|---|
| metric | object | 模型要最大化的度量。 | |
| learning_rate | float | 学习率 | 0.1 |
| n_estimators | int | 提升阶段数量,即简单模型的数量(决策树) | 100 |
| max_depth | int | 单个回归估计器的最大深度。最大深度限制了树中节点数量,通过调整该参数来优化性能。如果max_leaf_nodes不为空则忽略该参数。 |
3 |
| min_samples_split | int | 拆分内部节点所需的最小样本数。 | 2 |
| min_samples_leaf | int | 叶节点所需的最小样本数。 | 1 |
| subsample | float | 用于拟合单个基础学习器的样本比例。 | 1.0 |
| query_subsample | float | 用于拟合单个基础学习器的查询比例。(即qid数量) | 1.0 |
| max_features | int,float,string,none | 内部节点生成子节点时考虑的特征数量。(在存在大量特征时加速)。int时,表示要考虑的数量。float时,表示所有节点的百分比,auto时为sqrt(n_features),sqrt和auto一样,log2为($log_2{n_features}$),none时为所有特征均要考虑。选择“max_features < n_features”会导致方差减少和偏差增加。注意:在找到至少一个节点样本的有效分区之前,分割的搜索不会停止,即使它检查已经超过 max_features 个特征。 |
none |
| max_leaf_nodes | int/none | 生成树的最大叶节点数量。如果是none,则表示无限制。不为none时将忽略参数max_depth |
none |
| verbose | int | 启用详细输出。 如果为 1,则它会不时打印进度和性能(树越多频率越低)。 如果大于 1,则它会打印每棵树的进度和性能。 | 0 |
| warm_start | bool | 当设置为 True 时,重用之前调用 fit 的集成模型并向集成添加更多估计量,否则,只需删除之前的解决方案。 |
false |
| random_state | int,RandomState instance,none | 如果是 int,random_state 是随机数生成器使用的种子; 如果是 RandomState 实例,random_state 是随机数生成器; 如果没有,随机数生成器是 np.random 使用的 RandomState 实例。 |
none |
上述是初始化LambdaMART的参数,用于定义如下生成模型。除了这些参数以外,还包含如下的内部属性:
| 属性 | 类型 | 含义 |
|---|---|---|
| feature_importances_ | n_features纬数组 | 特征重要性(越高,特征越重要)。 |
| oob_improvement_ | n_estimators纬数组 | 袋外样本相对于前一次迭代的损失(= 偏差)改进。oob_improvement_[0] 是对 init 估计器的第一阶段损失的改进。 |
| train_score_ | n_estimators纬数组 | 第 i 个分数 train_score_[i] 是模型在迭代 i 时在袋内样本上的偏差(= 损失)。如果 subsample == 1 这就是训练数据的偏差。 |
| estimators_ | [n_estimators, 1]的ndarray存储训练完成的决策树集合 | 拟合子估计量的集合。 对于二元分类,loss_.K 为 1,否则为 n_classes。 |
| estimators_fitted_ | int | 实际拟合的子估计量的数量。 这可能与 n_estimators 在提前停止、修剪等情况下不同。 |
metric
进行训练效果的度量,这里使用的是NDCG,其定义如下:
1 | class NDCG(Metric): |
其中k表示只计算排序前k的数据的NDCG。gain_type表示度量NDCG是,每个文档的加权值,可以选择:
exp2表示使用的算分函数为:
identity表示使用的函数为:
执行fit(拟合)函数
1 |
|
1 | def _fit_stages(self, X, y, sample_weight, qids, y_pred, random_state, |
执行的训练函数
1 | def _fit_stage(self, i, X, y, qids, y_pred, sample_weight, sample_mask, |
获取lambda及相对于当前模型的梯度
这里计算算法介绍中的$\lambda_i$和$w_i$。
其执行逻辑为:
1 | # 输入为qid,y为样本真实label,y_pred为模型训练的输出label,y, y_pred均为一维数组 |
这里的lambda是负梯度,deltas是正常的lambda对$s_i$的导数。
计算互换位置后NDCG值
1 | def calc_swap_deltas(self, qid, targets): |
更新模型
1 | def _update_terminal_regions(self, tree, X, y, lambdas, deltas, y_pred, |
注意,这里
预测
训练完成后,或者验证时,执行预测的函数如下:
1 | def predict(self, X): |
终止训练判断
1 | class ValidationMonitor(object): |
其中参数trim_on_stop表示是否允许提前终止,stop_after表示当前训练的轮数,与效果最好的一轮之间差的轮数如果超过该值则停止训练(trim_on_stop为true时)。
具体终止判断的逻辑如下:
1 | # 返回true表示终止训练 |
日志输出
日志输出类如下:
1 | class _VerboseReporter(object): |
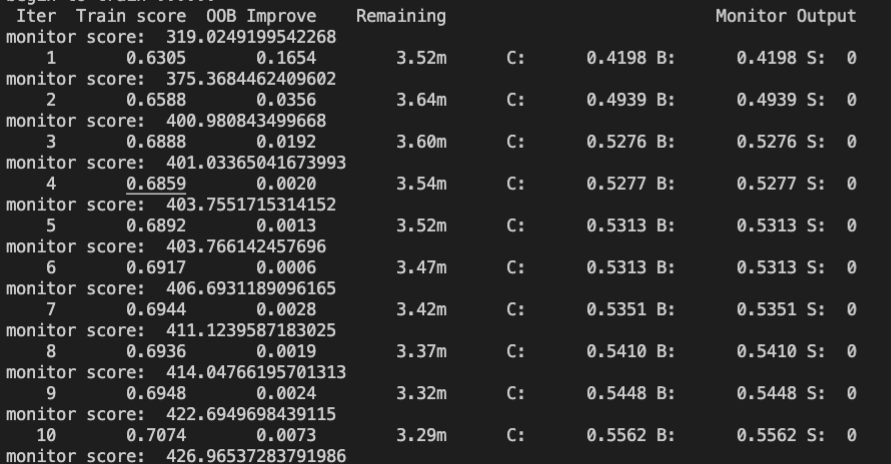
输出信息如下:
其中输出的每个字段含义如下:
| 字段 | 含义 |
|---|---|
| Iter | 迭代轮数 |
| train score | 平均的NDCG分数(越高约好) |
| OOB Improve | 每次与上一步迭代提升的train_score,即delta train_score; |
| Remaining | 根据当前训练轮数和花费时间预估训练完成时间 |
| C | 验证集的平均NDGC |
| B | 历次迭代中验证集中最高的平均NDGC |
| S | 迭达到当前步数,距离验证集最高的平均ndgc迭代步数的差(i-best_socre_i) |
存储模型并输出相关效果
使用pickle包存储模型。
1 | def save_model(model, file): |
输出每个因子的重要性。
1 | id2featrue = {} |
其中中存储了featureid到featurename的映射关系:
1 | ctr_norm 0 |
模型转换
gbrank只支持gbrank模型,因此需要将训练完成的lambdaMART模型进行一下转换。
修改notes/bin/trans_model_format.sh中的输入和输出模型即可。
执行对应脚本即获得可以直接在vsrank中使用的模型。