敏感词过滤
使用字典树+KMP算法。字典的子节点使用hashmap以加速。在字典中的每个节点中增加KMP中的偏移。为了使得可以匹配出多个字符,可以在字典树的根节点也设置偏移,解决类似如下情况
1 | 敏感词: |
在根节点中设置偏移,可以查询出全部出现的两个敏感词。
为了能够处理出现多个词才会命中的情况,例如
1 | 敏感词: |
即出现这两个时才过滤掉。这时,可以在根节点建立一个字典,其中key表示第几个干预词,value表示需要出现的term数量。这是为了解决如下情况的问题
1 | ABC&DEF |
此时对于DEF字典树的终节点(F)就有应该是{1:2, 2:2}。这里表示,第一个敏感词过滤需要两个term(其自身为其中一个),第二个敏感词过滤也需要两个。
中文切词
参考jieba做的中文切词,jieba存在两种方式。一个是词典查找,另一个是hmm(隐马尔可夫链)。
生成式与判别式
在机器学习中任务是从属性X预测标记Y,判别模型求的是P(Y|X),即后验概率;而生成模型最后求的是P(X,Y),即联合概率。从本质上来说:
判别模型之所以称为“判别”模型,是因为其根据X“判别”Y;
而生成模型之所以称为“生成”模型,是因为其预测的根据是联合概率P(X,Y),而联合概率可以理解为“生成”(X,Y)样本的概率分布(或称为 依据);具体来说,机器学习已知X,从Y的候选集合中选出一个来,可能的样本有$(X,Y_1), (X,Y_2), (X,Y_3),……,(X,Y_n)$,实际数据是如何“生成”的依赖于P(X,Y),那么最后的预测结果选哪一个Y呢?那就选“生成”概率最大的那个。
对于使用生成式,其实求取的是间接的P(Y|X)。由于
对于P(X)来说,由于X为输入,对于所有的输出Y来说,P(X)是一样的,因此,求P(X,Y)的最大就是求P(Y|X)的最大值。而且在生成式中相对来说,P(X|Y)和P(Y)更容易获取到,所以使用生成式来间接求取P(Y|X)。
假设有四个samples(x为输入,y为输出):
| sample1 | sample1 | sample1 | sample1 | |
|---|---|---|---|---|
| x | 0 | 0 | 1 | 1 |
| y | 0 | 0 | 0 | 1 |
生成式模型的世界是这个样子:
| y=0 | y=1 | |
|---|---|---|
| x=0 | 1/2 | 0 |
| x=1 | 1/4 | 1/4 |
即:
求取的是联合概率分布。
而判定式模型的世界是这个样子:
| y=0 | y=1 | |
|---|---|---|
| x=0 | 1 | 0 |
| x=1 | 1/2 | 1/2 |
即判别式求取的是条件概率分布。
生成式求解
定义训练集为(C,X),C={c1,c2,…cn}是n个样本的label,X={x1,x2,…xn}是n个训练样本的feature,定义单个测试数据为(c,x)。
训练完成后,输入测试数据,判别式直接给出P(c|x),即输出(label)关于输入(feature)的条件分布,实际上,这个分布的条件还有训练数据,因为实际上我们是“看过”训练数据之后,学习到了对数据分布的后验认识,然后根据这个认识和测试样本的feature来做出测试样本属于哪个label的决策的,所以有
即依据训练集训练出最大准确率的模型进行使用。
判别式求解
给定输入x,生成模型可以给出输入和输出的联合分布。生成方法的目标是求出这个联合分布。这里以朴素贝叶斯模型为例,我们要求的目标可以通过:
这样将求联合分布的问题转化成了求类别先验概率和类别条件概率的问题,朴素贝叶斯方法做了一个较强的假设————feature的不同维度是独立分布的,简化了类别条件概率的计算。
词典切词方式(Uni-gram)
首先建立词槽字典,比如如下样式:
1 | ... |
这里,前面是词槽,后面是出现概率。
导入该词典配置,建立一个前缀词词典。这里我觉得建立一个字典树更合适,在词典的最后一个子中标识为终点,并且包含其概率。
之后对待切词的文本进行前缀词查找,即将待匹配的文本的每一个字符作为起始字符,在前缀词典中进行前缀匹配查找,对于字典树来说,需要遍历到所以节点(保证找到所有的切词,而不能是找到一个末尾节点就直接返回)。为了加快速度,字典树中,子节点可以使用hashmap进行存储。这样可以直接进行查找,加快速度。此时对于待匹配的文本,会生成一个有向无环图,例如:
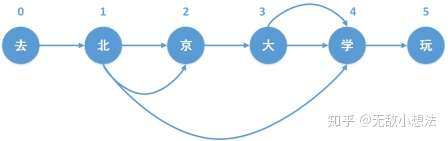
对于每一个字符,其存储的是从当前节点到切词末尾节点的边。对于上图的存储大致为:
1 | 0: [0] |
存储末尾位置的同时,也要存储对应的概率,这是为了计算最优路径。
构建了有向无环图后,就可以找到从起始到末尾的多条可选路径。这时,我们可以使用动态规划求解概率最大路径,其中转移函数为:
1 | dp[i] = max(dp[k] + p[i][k]) |
其中k为从节点i出发可以到达的节点k。但由于我们只存储了由前到后的边,未存储从后到前的节点,因此在动态规划时,需要从最后一个节点进行计算。在进行计算最大概率路径同时存储最优路径,当计算到第一个节点时即获取到最优切词结果。
HMM(隐马尔可夫链)
上述的方法只能处理在词典中出现的词,对于词典中未出现的词其效果很差。因此这里可以使用HMM来处理未出现在词典中的query(出现未出现都可以)。
HMM是生成式。
利用HMM模型进行分词,主要是将分词问题视为一个序列标注(sequence labeling)问题,其中,句子为观测序列,分词结果为状态序列。首先通过语料训练出HMM相关的模型,然后利用Viterbi算法进行求解,最终得到最优的状态序列,然后再根据状态序列,输出分词结果。
序列标注,就是将输入句子和分词结果当作两个序列,句子为观测序列,分词结果为状态序列,当完成状态序列的标注,也就得到了分词结果。
每个字处在词语中的4种可能状态,B、M、E、S,分别表示Begin(这个字处于词的开始位置)、Middle(这个字处于词的中间位置)、End(这个字处于词的结束位置)、Single(这个字是单字成词)。
使用HMM基于两点假设(s为状态,o为观测):
齐次马尔科夫性假设,即假设隐藏的马尔科夫链在任意时刻t的状态只依赖于其前一时刻的状态,与其它时刻的状态及观测无关,也与时刻t无关;
观测独立性假设,即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其它观测和状态无关,
对于隐马尔科夫讲解可以看下如下文档:
https://zhuanlan.zhihu.com/p/31926943
https://zhuanlan.zhihu.com/p/31943292
https://zhuanlan.zhihu.com/p/31999081
https://zhuanlan.zhihu.com/p/32080000
最终我们求解的是对于给定的观察序列O(o1,o2,…oT,获取其与状态序列I(s1,s2,…sT)的联合分布概率最大值,即
由于
将O递归拆分为AB两部分,第一次划分如下:
观测独立性假设,上式变换为
之后递归的对上式中前一部分进行拆分
通过不断递归拆分,最终得到
所以
对于P(I)来说
由于齐次马尔科夫性假设
之后对上式中后半部分继续执行上述变换,则得到
于是,得到最终的概率函数
所以使用HMM我们需要知道三部分值:
- P(oi|si):发射概率。当处于状态si时,观察值(即字符为oi)的概率。
- P(Si-1|si): 转移概率。即对于i-1的状态为si-1时,i的状态为si的概率。
- P(s1): 初始状态概率。即第一个字符为状态s1的概率。
上述3部分值的获取就是对HMM模型的训练,jieba获取方式是拿98年报纸和其他杂志信息中的切词,统计词频,获取对应每一部分的概率。这三部分概率均存储于文件中,对应格式如下。概率值都是取对数之后的结果(可以让概率相乘转变为概率相加),其中-3.14e+100代表负无穷,对应的概率值就是0。
发射概率
1
2
3
4
5
6
7
8P={'B': {'一': -3.6544978750449433,
'丁': -8.125041941842026,
'七': -7.817392401429855,
...
'S': {':': -15.828865681131282,
'一': -4.92368982120877,
'丁': -9.024528361347633,
...P[‘B’][‘一’]代表的含义就是状态处于’B’,而观测的字是‘一’的概率对数值为P[‘B’][‘一’] = -3.6544978750449433
转移概率
1
2
3
4P={'B': {'E': -0.510825623765990, 'M': -0.916290731874155},
'E': {'B': -0.5897149736854513, 'S': -0.8085250474669937},
'M': {'E': -0.33344856811948514, 'M': -1.2603623820268226},
'S': {'B': -0.7211965654669841, 'S': -0.6658631448798212}}P[B][E]代表的含义就是从状态B转移到状态E的概率,由P[‘B’][‘E’] = -0.5897149736854513,表示当前状态是B,下一个状态是E的概率对数是-0.5897149736854513,对应的概率值是0.6,相应的,当前状态是B,下一个状态是M的概率是0.4,说明当我们处于一个词的开头时,下一个字是结尾的概率要远高于下一个字是中间字的概率,符合我们的直觉,因为二个字的词比多个字的词更常见。
初始状态概率
1
2
3
4P={'B': -0.26268660809250016,
'E': -3.14e+100,
'M': -3.14e+100,
'S': -1.4652633398537678}这个概率表说明一个词中的第一个字属于{B、M、E、S}这四种状态的概率,如下可以看出,E和M的概率都是0,这也和实际相符合:开头的第一个字只可能是每个词的首字(B),或者单字成词(S)。
获得这三部分数据后,通过Viterbi算法(动态规划的一种)。
假设给定隐式马尔可夫模型(HMM)状态空间S,共有k个状态,初始状态 i 的概率为 P(i) ,从状态i 到状态 j 的转移概率为 P[i][j]。 令观察到的输出为 y1,…yT。 产生观察结果的最有可能的状态序列 x1,….xT 由递推关系给出:
通过上述两式即可进行动态规划,在计算第二个式子是,存储下所选择的x,即选择的前一个节点的状态,即可直接在计算完成后获得最优状态序列。对于分词来说,最后一个子只可能是s或e,因此对于最后一个子,只需要比较其状态为s和e大小即可,选择较大者,即
前向后向算法评估观测序列概率
问题:已知HMM模型的参数$\lambda=(A,B,\Pi)$。其中𝐴是隐藏状态转移概率的矩阵,𝐵是观测状态生成概率的矩阵,$\Pi$是隐藏状态的初始概率分布。隐藏状态的状态空间为N。同时我们也已经得到了观测序列$O=\{o_1,o_2,…o_T\}$,现在我们要求观测序列𝑂在模型𝜆下出现的条件概率$P(O|λ)$。
暴力算法为
列出所有可能的I,求出每一个对应的$P(O,I|\lambda)$。但复杂度过高。对于含有N个隐藏状态的需求来说,其复杂度为$O(TN^T)$。
前向算法求解hmm观测序列概率
前向算法为动态规划算法,通过定义前向概率来定义动态规划这个局部状态,前向状态定义为:时刻t时隐藏状态为$q_i$,观测状态的序列为$o_1,o_2,…o_t$的概率,即
之后,进行t+1状态的递推。基于时刻t的各个隐藏状态的前向概率,再乘以对应的状态转移概率,即${\alpha}_t(j)a_{ji}$就是时刻t观测到$o_1,o_2,…o_t$,并且时刻t隐藏状态为$q_j$,时刻t+1隐藏状态为$q_i$的概率。即
将所有的t时刻隐藏状态乘以对应的转移概率,并进行求和:
即得到时刻t观测序列为$o_1,o_2,…o_t$,并且时刻t+1时刻隐藏状态为$q_i$的概率。由于观测状态只依赖于t+1时刻的隐藏状态$q_i$,因此:
因此,我们就得到了递推公式,即
动态规划从1开始,到时刻T结束,${\alpha}_T(i)$表示在时刻T关系序列为$o_1,o_2,…o_T$,并且时刻T隐藏状态为$q_i$的概率,所以,只要将所以隐藏状态对于的概率相加,即$\sum_{i=1}^N{\alpha}_T(i)$即得到时刻T观测序列为$o_1,o_2,…o_T$的概率。
总结前向算法:
输入:HMM模型$\lambda=(A,B,\Pi)$,观测序列$O=(o_1,o_2,…o_T)$
输出:观测序列概率$P(O|\lambda)$。
计算时刻1的各个隐藏状态前向概率:
递推时刻2,3,…T时刻的前向概率:
计算最终结果:
从递推公式可以看出,其时间复杂度为$O(TN^2)$。
后向算法求解HMM观测序列概率
后向算法与前向算法类似,也是使用动态规划求解,不过选择的局部状态为后向概率,后向概率为:
递推公式为:
后向算法步骤为:
输入:HMM模型$lambda=(A,B,\Pi)$,观测序列$O=(o_1,o_2,…o_T)$。
输出:观测序列概率$P(O|\lambda)$
初始化时刻T的各个隐藏状态后向概率:
递推时刻T-1,T-2,…1时刻的后向概率:
计算最终结果:
其复杂度为$O(TN^2)$。
HMM常用概率的计算
给定模型$\lambda$和观测序列$O$,在时刻t处于状态$q_i$的概率记为:
由于
因此:
给定模型$\lambda$和观测序列$O$,在时刻$t$处于状态$q_i$,且时刻t+1处于状态$q_j$的概率记为:
由于
因此
EM(期望极大算法)
EM算法用于含有隐变量的概率模型的极大似然估计或极大后验概率估计。EM算法分为两步:E步,求期望(expection);M步,求极大(maximization)。
一般的,将Y表示为观察随机变量的数据,Z表示隐随机变量的数据。Y和Z连在一起称为完全数据。假设Y和Z的联合概率分布为
则完全数据的对数似然函数为
EM算法通过迭代求解
的极大似然估计,来优化参数。
EM算法
输入:观测变量Y,隐变量数据Z,联合分布$P(Y,Z|\theta)$,条件概率分布$ P(Z|Y,\theta)$;
输出:参数模型$ \theta$;
(1)选择参数初始值$ {\theta}^{(0)}$,开始迭代。
(2)E步:记$ {\theta}^{(i)} $为第i次迭代参数$\theta$的估计值,在第$i+1$次迭代的E步,计算
其中$P(Z|Y,{\theta}^{(i)})$是在给定观测数据Y和当前的参数估计${\theta}^{(i)}$下隐变量Z的条件概率分布。
(3)M步:求使得$Q(\theta,{\theta}^{(i)})$极大化的$\theta$,确定第i+1次迭代的参数的估计值${\theta}^{(i+1)}$
(4)重复2,3两步,直到收敛。
Q函数为:完全数据的对数似然函数$logP(Y,Z|\theta)$关于在给定观测数据Y和当前参数${\theta}^{(i)}$下对未观测数据Z的条件概率分布$P(Z|Y,{\theta}^{(i)})$的期望称为$Q$函数,即
几点注意:
EM算法对初值敏感
迭代停止条件,一般是对较小的正数${\epsilon}_1,{\epsilon}_2$,满足
EM算法的导出(可行性证明)
对于含有隐变量的概率模型,目标是极大化观测数据(不完全数据)Y关于参数$\theta$的对数似然函数,即:
假设第i次迭代后$\theta$的估计值为${\theta}^i$,希望新的估计值增加,即$L(\theta) > L({\theta}^i)$,并逐步达到最大值,此时,考虑二者差值:
利用Jensen不等式
得到
由于
因此
令
则
函数$B(\theta,{\theta}^i)$是$L(\theta)$的下界,并且根据上面的式子可得$L({\theta}^i) = B(\theta,{\theta}^i)$。任何使得B增大的$\theta$,也可以使得$L(\theta)$增大,选择${\theta}^{i+1}$使得B达到最大,即
省区对$\theta$的极大化而言是常数的项,则
EM算法生成HMM参数(鲍姆-韦尔奇算法)
训练数据为$\{(O_1,I_1),(O_2,I_2),…(O_D,I_D)\}$,其中任意观测序列$O_d=\{o_1^d,o_2^d,…o_T^d\}$,其对应的未知的隐藏状态序列为$I_d=\{i_1^d,i_2^d,…I_T^d\}$。
算法E步,先计算联合分布$P(O,I|\lambda)$,表达式如下:
其中${\pi}_i$为初始状态概率,$b_i(o)$为发射概率,$a_{i_1,i_2}$为转移概率。
E步中我们求取期望为
在M步中,我们要极大化上式,$P(I|O,\overline{\lambda})=\frac{P(I,O|\overline{\lambda})}{P(O|\overline{\lambda})}$,而$P(O|\overline{\lambda})$为常数,因此要极大化的式子等价于
隐藏参数$\lambda=(A,B,\Pi)$,上式分别对$A,B,\Pi$求导可得更新的参数模型$\overline{\lambda}$。
首先看模型参数$\Pi$的导数。由于$\Pi$只在第一部分出现,因此
由于${\pi}_i$还满足$\sum_{i=1}^N{\pi}_i=1$,根据拉格朗日子乘法,我们得到${\pi}_i$要极大化的拉格朗日函数为
其中$\gamma$为拉格朗日系数,上式对${\pi}_1$求偏导,并令结果为0,得到
令i从1到N,从上式可以得到N个式子,对N个式子求和可得
上面两式消去$\gamma$得
再来看$A$的迭代公式,方法和$\Pi$的类似,由于$A$只在最大化函数里的第二部分出现,因此:
由于$a_{ij}$满足$\sum_{j=1}^Na_{ij}=1$。因此要最大化的式子为:
对上式的$a_{ij}$求偏导,并使导数为0,得:
与${\pi}_i$类似,对所有N个式子求和可得:
因此:
最后看B的迭代公式:
又由于$\sum_{k=1}^Mb_j(o_t=v_k)=1$,因此,与求a时类似:
只有在$o_t=v_k$时,$b_j(o_t)$对$b_j(k)$的偏导数才不为0,使用$I(o_t=v_k)$表示,因此对上式求导得:
与之前类似,对所有M个式子求和,得到:
因此:
由此,我们得到了模型$\lambda=(A,B,\Pi)$迭代公式。
总结整体流程:
输入:D个观察样本$\{O_1,O_2,…O_D\}$
输出:HMM模型参数
随机初始化所有${\pi}_i,a_{ij},b_j(k)$。
对每个样本$d=1,2,…D$,用前向后向算法计算${\gamma}_t^d(i),{\xi}_{t}^d(i,j);t=1,2,…T;i=1,2…N;j=1,2,…N$。
更新模型参数:
如果参数值已收敛,则停止迭代,输出模型,否则重复2,3步。