计算几何学

Posted on | In |
Words count in article: | Reading time ≈
计算机几何学是面试时常会被问起的问题，当然也十分考验思维能力.很久之前就想要写这篇博客了，之前一直没有时间，终于在这个十一假期不上了，感谢国庆，共产党万岁！！！

计算几何学

叉积

叉积的计算是线段方法的核心。叉积被解释为由点(0,0)，p1，p2，和p1+p2=(x1+x2,y1+y2)所构成的平行四边形的有向面积。p1*p2 = x1*y2-x2*y1。结果的正负代表方向。其中方向符合右手定则。即用右手从p1出发，沿小于180度的方向向p2握拳，此时大拇指的朝向即为叉积方向。这里大拇指向上表示正方向（叉积为正），大拇指向下表示负方向（叉积为负）。

利用叉积，我们立刻可以得出一个简单的性质。若p1*p2大于０，则相对于原点来说，p1位于p2的顺时针方向，若叉积为负，则p1位于p2的逆时针方向。如果是零，则三点共线。

在上述基础上延伸，可得到相对与公共端点p0, p1是位于p2的顺时针还是逆时针方向（考虑的都是小于等于180读，即顺时针还是逆时针更接近）。此时只需要求向量$p_0p_1$与$p_0p_2$的叉积即可。

连续线段是向左转还是向右转

两条连续线段，求$p_0p1$和$p_1p_2$在p1点选择方向。利用上述的相对与公共端点的另外两个点的位置关系即可求出。在这里以p0为公共端点，求p1与p2的位置关系。

两条线段是否相交

判断两条线段是否相交，可以向考虑一个点是在一条直线的左侧还是右侧。如果能够获得次结果，则两条直线相交的条件是，任一条线的两个端点在另一条线的两侧（或者恰巧在线上）。此时再来考虑如何确定一个点是在线段的那一侧。这时我们可以发现，我们依然可以利用相对与公共端点的另外两个点的位置关系。在这里，我们以直线的任意一个端点作为公共端点，求另外两个点的位置关系。这里不必获得具体的点在直线的左侧还是右侧，因为选取不同线段端点为公共端点会产生不同的结果，而且没有必要确定在哪一测，我们只需要判断一条线段的两个端点是否在另一条线段的两侧即可，此时我们在判断Ａ线段的两个端点是否在Ｂ线段两侧时，我们只用保证选择的Ｂ的公共端点一致即可。如果选择公共端点一致，而对Ａ的两个端点相对于线段Ｂ得出来的叉积符号相反就说明在Ａ的两个端点在线段Ｂ的两侧。还有一个特殊情况就是一个线段的端点恰巧在另一条线段上，此时叉积为０。在叉积为０时确定点是否在线上是是否简单的，因为此时只有两种情况，一种是点在线上，另一种是点在线段延长线上。此时判断只需比较坐标大小即可。由此可得如下程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
struct points
{
    int x;
    int y;
};
int direction(points p1, points p2, points p3)
{
    int x1 = p3.x-p1.x;
    int y1 = p3.y-p1.y;
    int x2 = p2.x-p1.x;
    int y2 = p2.y-p1.y;
    return x1*y2 - x2*y1;
}
bool on_lines(points p1, points p2, points p3)
{
    int max_x = p1.x>p2.x?p1.x:p2.x;
    int min_x = p1.x>p2.x?p2.x:p1.x;
    int max_y = p1.y>p2.y?p1.y:p2.y;
    int min_y = p1.y>p2.y?p2.y:p1.y;
    if(p3.x >= min_x && p3.x<=max_y && p3.y>=min_y && p3.y<=max_y)
    {
        return 1;
    }
    else
    {
        return 0;
    }
    
}
bool segment_intersect(points p1, points p2, points p3, points p4)
{
    int d1 = direction(p1,p2,p3);
    int d2 = direction(p1, p2, p4);
    int d3 = direction(p3, p4, p1);
    int d4 = direction(p3, p4, p2);
    if(d1*d2<0 && d3*d4<0)
    {
        return 1;
    }
    if(d1==0 && on_lines(p1,p2,p3))
    {
        return 1;
    }
    if(d2==0 && on_lines(p1,p2,p4))
    {
        return 1;
    }
    if(d3==0 && on_lines(p3,p4,p1))
    {
        return 1;
    }
    if(d4==0 && on_lines(p3,p4,p2))
    {
        return 1;
    }
    return 0;
}

确定任意一对线段是否相交

对于ｎ条线段，确定两条线段是否相交，如果使用最简单的方法，即每两个线段相比较，则复杂度将会是Ｏ(n^2)这在线段较多的时候显然是无法接受的，于是这里提出了一个“扫除”的操作，可以使得复杂度降低到O(nlogn)。具体解释如下：

在扫除过程中，一条假想的扫除线穿过一个给定的几何物体集合，并且通常是从前先后扫除。我们将线段的端点按照从左向右排序，在扫除线移动的过程中，遇到线段的端点就判断相关线段是否相交。

线段排序

我们将在扫除线处，对与扫除线相交的线段进行排序，排序的规则是与扫除线交点的ｙ坐标(这里假设不存在竖直的线，实际算法中存在竖直线也是无所谓的。)。将ｙ坐标的高的放上方。当扫除线在ｘ时，两条线段都与扫除线相交，则称这两条线是在ｘ可比较的，就可以使用上述方法进行排序。在扫除线遇到线段左端点时就将该线段加入排序，当扫除线遇到右端点时从排序中删除。在不同ｘ处排序完全前序可能不同，如果存在两条线段，随着扫除线的移动，排序顺序由Ａ>B变成B>=A，则说明线段相交。

移动扫除线

扫除线算法要维护两组数据：

１．扫除线状态：给出了与扫除线相交的物体之间的关系。

２．时间点调度：是一个按照ｘ坐标从左到右排序的时间点序列。随着扫除线的移动，每当遇到时间点的ｘ坐标就会停止，处理事件，然后重新扫除，扫除线状态只会在时间点出改变。

程序流程

１．首先将线段端点集合进行从左到右排序。在这里，如果两个点的ｘ坐标一致，则左端点的排在前面(这是为了处理两条线段在端点处相交)，如果ｘ一致，且都是同一类型的端点(左右)则将ｙ低的放前面。

２．初始化一个空的线段排序集合。这里为了保证速度更快，使用红黑树来实现排序，将比较方式换成线段排序部分所描述的。这里直接判断交点ｙ坐标是不可取的(麻烦且不准确)，依然可以利用叉积进行判断。在判断线段相交是，我们会判断一个线段的两个端点是否在另一条线段的两边。这里的判断与之类似，如果一个线段Ａ的端点的两个端点在另一条线段Ｂ的同一侧时，我们可以判断出Ａ整体是在Ｂ的上方或者下方，此时在ｘ处的两条线段与扫除线的交点ｙ坐标就也确定了。如果两条线段不相交，则一定会出现这种情况，如果两条线段相交当然可以直接返回，说明存在线段相交，但如果使用STL中的红黑树，则不存在这种操作(其实是有的，可以定义一个static类型，当在判断函数中两条线段相交，则将该值置一，每次插入是，检查插入后该值是否变成１了)。此时，由下面的流程可知，其实只会在线段的左端点进行排序操作（其实在删除时也会进行排序，但不影响程序的准确性），此时只需判断两条线段的左端点的ｙ坐标，那个高则哪个在上。

３．不断取出从第一步中的排序好的点，判断端点类型，如果是左端点，则将该线段插入线段排序集合中，同时，取出其上下两条线段(如果存在)，分别与该线段判断是否相交，如果相交，则结束。否则继续扫除。如果是右端点，则取出其上下两条线段(如果存在)，判断上下两条线是否相交，如果相交则结束，否则从排序集合中删除该线段继续操作。如果一直到所以线段都添加后删除了，依然没有两条线段相交，则说明不存在两条线段相交。

正确性

命题：该方法能够正确判断线段相交。

我们需要证明该命题的充分必要性。

充分性

即该方法确定存在线段相交则必然存在线段相交。这是很显然的，因为我们在判断线段相交时是使用了基本的线段相交算法，因此如果该算法判断线段相交，则必然存在线段相交。

必要性

即如果存在线段相交，则该方法一定可以检测出来。假设线段Ａ，Ｂ相交，在其中一条线Ａ已近加入排序集合的情况下，Ｂ进入集合会存在两种情况。１．与线段Ａ排序相邻，此时由于插入时会判断与插入直线相邻的线段关系，直接可以得出线段相交。２．在Ａ与Ｂ之间存在线段Ｃ(之间存在多条线段与存在一条是类似的)，由于Ｃ不与这两条线相交，则在Ａ，Ｂ交点前Ｃ已被移除排序集合。此时，由于移除集合时会判断被移除的线段上下两条线段是否相交，此时也能够获得线段相交。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
#include <iostream>
#include <set>
using namespace std;
struct lines;
struct points
{
    int x;
    int y;
    bool lor; // 0 is right, 1 is right
    lines *ln;
};
struct lines
{
    points left;
    points right;
};
bool compare1(points *p1, points *p2)
{
    if (p1->x < p2->x)
    {
        return 1;
    }
    else
    {
        if (p1->x > p2->x)
        {
            return 0;
        }
        else
        {
            if (p1->lor == 0 && p2->lor == 1)
            {
                return 1;
            }
            else
            {
                if (p1->lor == 1 && p2->lor == 0)
                {
                    return 0;
                }
                else
                {
                    if (p1->y < p2->y)
                    {
                        return 1;
                    }
                    else
                    {
                        return 0;
                    }
                }
            }
        }
    }
}
bool points_stay(points p1, points p2, points p3)
{
    int x1 = p2.x - p1.x;
    int x2 = p3.x - p1.x;
    int y1 = p2.y - p1.y;
    int y2 = p3.y - p1.y;
    int ret = x1 * y2 - x2 * y1;
    if (ret > 0)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}
// l1在l2上⾯则返回0，l1在l2下⾯则返回1，l1在l2上⾯且相交则返回3，l1在l2下⾯且相交则返回4
int line_context(lines l1, lines l2)
{
    int d1 = points_stay(l1.left, l1.right, l2.left);
    int d2 = points_stay(l1.left, l1.right, l2.right);
    int d3 = points_stay(l2.left, l2.right, l1.right);
    int d4 = points_stay(l2.left, l2.right, l1.right);
    if ((d1 > 0 && d2 > 0) || (d3 < 0 && d4 < 0))
    {
        return 0;
    }
    if ((d1 < 0 && d2 < 0) || (d3 > 0 and d4 > 0))
    {
        return 1;
    }
    if (l1.left.y >= l2.left.y)
    {
        return 3;
    }
    return 4;
}
bool compare2(lines *l1, lines *l2)
{
    int ret = line_context(*l1, *l2);
    if (ret == 0 || ret == 3)
    {
        return 1;
    }
    return 0;
}
int main()
{
    int n;
    cin >> n;
    lines *ln = new lines[n];
    points *ps = new points[2 * n];
    points p1, p2;
    set<points *, bool (*)(points *, points *)> stat(compare1);
    for (int i = 0; i < n; i++)
    {
        cin >> p1.x >> p1.y >> p2.x >> p2.y;
        if (p1.x < p2.x || ((p1.x == p2.x) && (p1.y < p2.y)))
        {
            p1.lor = 0;
            p2.lor = 1;
            p1.ln = &(ln[i]);
            p2.ln = &(ln[i]);
            ln[i].left = p1;
            ln[i].right = p2;
        }
        else
        {
            p1.lor = 1;
            p2.lor = 0;
            p1.ln = &(ln[i]);
            p2.ln = &(ln[i]);
            ln[i].left = p2;
            ln[i].right = p1;
        }
        ps[2 * i] = p1;
        ps[2 * i + 1] = p2;
        stat.insert(&(ps[2 * i]));
        stat.insert(&(ps[2 * i + 1]));
    }
    for (auto i = stat.begin(); i != stat.end(); i++)
    {
        points *w = *i;
        cout << w->x << " " << w->y << " " << w->lor << endl;
    }
    bool is_seg = 0;
    set<lines *, bool (*)(lines *, lines *)> sort_line(compare2);
    for (auto i = stat.begin(); i != stat.end(); i++)
    {
        points p = **i;
        lines *l = p.ln;
        if (p.lor == 0)
        {
            sort_line.insert(l);
            lines *l1 = NULL;
            if (sort_line.lower_bound(l) != sort_line.end())
            {
                lines *l1 = *(sort_line.lower_bound(l));
            }
            if (l1 != NULL && l1 != l)
            {
                int w = line_context(*l1, *l);
                if (w == 3 || w == 4)
                {
                    is_seg = 1;
                    cout << "seg\n lin1:" << l->left.x << " " << l->left.y << " " << l->right.x << " " << l->right.y << endl;
                    cout
                        << "line2:" << l1->left.x << " " << l1->left.y << " " << l1->right.x << " " << l1->right.y << endl;
                    delete[] ps;
                    delete[] ln;
                    break;
                }
            }
            lines *l2 = NULL;
            if (sort_line.upper_bound(l) != sort_line.end())
            {
                l2 = *sort_line.upper_bound(l);
            }
            if (l2 != NULL && l2 != l)
            {
                int w = line_context(*l2, *l);
                if (w == 3 || w == 4)
                {
                    is_seg = 1;
                    cout << "seg\n lin1:" << l->left.x << " " << l->left.y << " " << l->right.x << " " << l->right.y << endl;
                    cout << "line2:" << l2->left.x << " " << l2->left.y << " " << l2->right.x << " " << l2->right.y << endl;
                    delete[] ps;
                    delete[] ln;
                    break;
                }
            }
        }
        else
        {
            lines *l1 = NULL;
            if (sort_line.lower_bound(l) != sort_line.end())
            {
                lines *l1 = *(sort_line.lower_bound(l));
            }
            lines *l2 = NULL;
            if (sort_line.upper_bound(l) != sort_line.end())
            {
                l2 = *sort_line.upper_bound(l);
            }
            if (l1 != NULL && l2 != NULL && l1 != l2)
            {
                int w = line_context(*l1, *l2);
                if (w == 3 || w == 4)
                {
                    is_seg = 1;
                    cout << "seg\n lin1:" << l1->left.x << " " << l1->left.y << " " << l1->right.x << " " << l1->right.y << endl;
                    cout << "line2:" << l2->left.x << " " << l2->left.y << " " << l2->right.x << " " << l2->right.y << endl;
                    delete[] ps;
                    delete[] ln;
                    break;
                }
            }
            sort_line.erase(l);
        }
    }
    cout << "way1:" << (is_seg ? "YES" : "NO") << endl;
    is_seg = 0;
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            int w = line_context(ln[i], ln[j]);
            if (w == 3 || w == 4)
            {
                is_seg = 1;
                break;
            }
        }
    }
    cout << "way2:" << (is_seg ? "YES" : "NO") << endl;
    return 0;
}

凸包

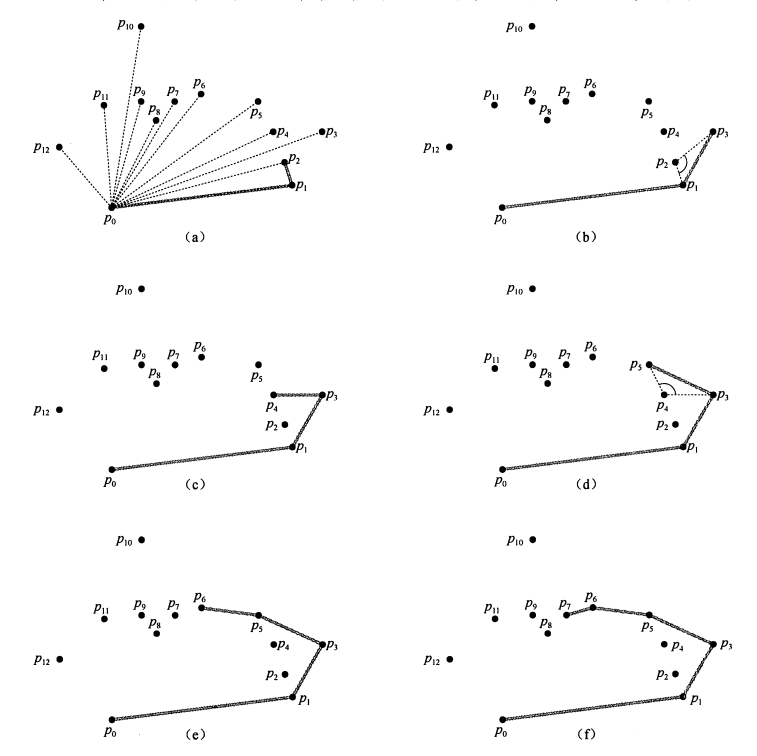
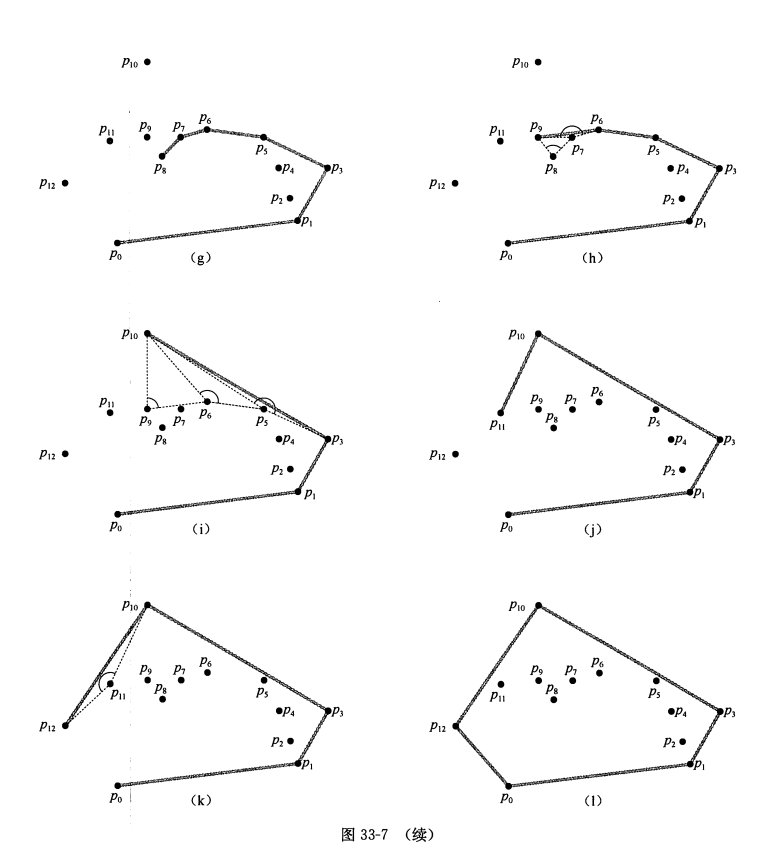
点集Ｑ的凸包是最小的一个凸多边形Ｐ，满足Ｑ中每个点都在Ｐ的边界上或者Ｐ的内部。凸包在计算机几何学中是十分有用的，例如我们可以利用凸包在Ｏ(n)（ｎ为凸包的边数）的时间复杂度下找到点集中距离最远的两个点。获取凸包有很多方法，复杂度都能够达到O(nlogn)(n为点的数目)。这里介绍的方法为Graham扫描法。

Graham扫描法通过维持一个关于候选点的栈来解决凸包问题。输入集合每个点都会被压入栈一次，非凸包的顶点最终会被弹出栈，最终栈中将只包含凸包的顶点。

程序流程：

１．首先选出凸包最下面的点，该点一定是ｙ坐标最小的点，如果有多个个点ｙ坐标一致，则找到ｘ坐标最小的点，这样，改点必然属于凸包的顶点。

２．将剩下来的点按照与第一步中选择的点为极点所成的极角进行排序，这里排序使用点在线段的左边这一判断方式即可。

３．将第一步选择的点压入一个栈中，将第二步中排序的第一个取出压入栈。之后依次取出第二步中排序的点，将该点与栈顶的两个点进行比较，判断是否三个点构成的两条线段是向左转，如果是，则直接将该点压入栈，否则删除栈顶元素，重复进行与栈顶两个元素进行的操作，如果一直删除到栈只剩下一个元素还没有向左转，则将该节点压入栈。这样依次对所以排序的节点指向上述操作。最终栈内元素即为凸包的顶点。

下图展示了操作流程：4TVjN8.png

4TZFH0.png

利用凸包获取点集中最远的两个点

显然距离最远的点一定是凸包中的点之间的距离。首先利用上面的Graham扫描法获得凸包。而后任选一条凸包的边，找到凸包中距离该边最远的点，寻找也可以使用叉积实现，沿着选择的边，逆时针查找凸包的边，相对于选择的线段（将选择的线段平移至与接下来进行比较的边共起点，使选择的边与比较的边共右端点），如果边是向右转的，则比较的线段对左端点是当前距离该线段最远的点，接着继续比较。直到遇到第一个是左旋的，此时该线段的右端点即为距离被选择的边最远的点。比较该点距离被选线段的两个端点哪个远并记录。而后逆时针依次寻找所有距离凸包边最远的点，利用边移动，对应的距离最远的点也同步移动，即选择的边是原被选边的右边，则距离该边最远的点是原来距离原被选的边的右边，则可以依次比较点到线段两个端点的距离。这样就可以找到最远两个点。

代码：凸包与点集中最远两个点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
#include <iostream>
#include <set>
#include <stack>
using namespace std;
struct points
{
    int x;
    int y;
};
static points start;

//按极角排序
bool compare1(points p1, points p2)
{
    int x1 = p1.x - start.x;
    int x2 = p2.x - start.x;
    int y1 = p1.y - start.y;
    int y2 = p2.y - start.y;
    int ret = x1 * y2 - x2 * y1;
    if (ret > 0)
    {
        return 1;
    }
    else
    {
        if (ret < 0)
        {
            return 0;
        }
        else
        {
            if (x1 * x1 + y1 * y1 > x2 * x2 + y2 * y2)
            {
                return 1;
            }
            else
            {
                return 0;
            }
        }
    }
}
int distant(points p1, points p2)
{
    return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
}
// 判断是否一条直线在另一条的右边
bool compare2(points p1, points p2, points p3)
{
    int x1 = p2.x - p1.x;
    int x2 = p3.x - p1.x;
    int y1 = p2.y - p1.y;
    int y2 = p3.y - p1.y;
    int ret = x1 * y2 - x2 * y1;
    if (ret > 0)
    {
        cout << "True" << endl;
        return 1;
    }
    else
    {
        cout << "Fals" << endl;
        return 0;
    }
}
int main()
{
    int n;
    cin >> n;
    points *all_points = new points[n];
    int start_index = -1;
    for (int i = 0; i < n; i++)
    {
        cin >> all_points[i].x >> all_points[i].y;
        if (start_index == -1 || start.y > all_points[i].y || (start.y == all_points[i].y && start.x > all_points[i].x))
        {
            start.x = all_points[i].x;
            start.y = all_points[i].y;
            start_index = i;
        }
    }
    //使用红黑树构建起始顺序
    set<points, bool (*)(points p1, points p2)> sort_points(compare1);
    for (int i = 0; i < n; i++)
    {
        if (i != start_index)
        {
            sort_points.insert(all_points[i]);
        }
    }
    cout << "sort:" << endl;
    for (auto i = sort_points.begin(); i != sort_points.end(); i++)
    {
        cout << (*i).x << " " << (*i).y << endl;
    }
    //使用Graham获取凸包
    stack<points> tubao;
    tubao.push(start);
    tubao.push(*sort_points.begin());
    for (auto i = ++sort_points.begin(); i != sort_points.end(); i++)
    {
        points p2 = tubao.top();
        tubao.pop();
        points p1 = tubao.top();
        tubao.push(p2);
        while ((compare2(p1, p2, *i) == 0) && tubao.size() > 1)
        {
            cout << "tubao.size= " << tubao.size() << endl;
            tubao.pop();
            if (tubao.size() > 1)
            {
                p2 = tubao.top();
                tubao.pop();
                p1 = tubao.top();
                tubao.push(p2);
            }
            else
            {
                break;
            }
        }
        tubao.push(*i);
    }
    //从凸包中利用
    int num = tubao.size();
    points *tubao_list = new points[num];
    for (int i = 0; i < num; i++)
    {
        tubao_list[num - i - 1] = tubao.top();
        tubao.pop();
    }
    int stand_x = tubao_list[1].x - tubao_list[0].x;
    int stand_y = tubao_list[1].y - tubao_list[0].y;
    int max_index = 2;
    for (int i = 2; i < num; i++)
    {
        max_index = i;
        points p;
        p.x = tubao_list[i - 1].x + stand_x;
        p.y = tubao_list[i - 1].y + stand_y;
        int case1 = compare2(tubao_list[i - 1], p, tubao_list[i]);
        if (case1 < 0)
        {
            max_index--;
            break;
        }
        else
        {
            if (case1 == 0)
            {
                int dis1 = distant(tubao_list[0], tubao_list[i]);
                int dis2 = distant(tubao_list[1], tubao_list[i]);
                int dis3 = distant(tubao_list[0], tubao_list[i - 1]);
                int dis4 = distant(tubao_list[1], tubao_list[i - 1]);
                if (((dis3 >= dis1) && (dis3 >= dis2)) || ((dis4 >= dis1) && (dis4 >= dis2)))
                {
                    max_index--;
                }
                break;
            }
        }
    }
    int max_dis = -1;
    points left;
    points right;
    for (int i = 1; i < num; i++)
    {
        if (distant(tubao_list[i - 1], tubao_list[max_index]) > max_dis)
        {
            max_dis = distant(tubao_list[i - 1], tubao_list[max_index]);
            left = tubao_list[i - 1];
            right = tubao_list[max_index];
        }
        if (distant(tubao_list[i], tubao_list[max_index]) > max_dis)
        {
            max_dis = distant(tubao_list[i], tubao_list[max_index]);
            left = tubao_list[i];
            right = tubao_list[max_index];
        }
        max_index++;
        max_index %= num;
    }
    cout << "max_dis1=" << max_dis << endl;
    cout << left.x << " " << left.y << endl;
    cout << right.x << " " << right.y << endl;
    max_dis = -1;
    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            int dis = distant(all_points[i], all_points[j]);
            if (dis > max_dis)
            {
                max_dis = dis;
            }
        }
    }
    cout << "max_dis2=" << max_dis << endl;
    max_dis = -1;
    for (int i = 0; i < num; i++)
    {
        for (int j = i + 1; j < num; j++)
        {
            int dis = distant(tubao_list[i], tubao_list[j]);
            if (dis > max_dis)
            {
                max_dis = dis;
            }
        }
    }
    cout << "max_dis3=" << max_dis << endl;
    return 0;
}

寻找点集中最近两个点之间的距离

最笨且可靠的方法，比较任意两个点之间的距离，确定最近距离。但这个方法的时间复杂度是O(n^2)。这显然是无法接受的。此时我们可以考虑使用空间换时间的方式，采用递归的方法进行计算。

基本思路为：将点集分别按照x坐标和y坐标排序。选择一条竖直线，将点集分为两组（竖线上的点可以随意分到左边或者右边），分别递归的获取两组点集的最小距离而后对两个点集进行合并操作。需要注意的是，在划分时，需要将分别按照x，y已排列好的集合进行划分，同时要保证划分到两个集合依然保持排序好的状态，这一点是很简单的，看代码就能明白。最关键的是合并的操作。分别获取两个集合的最小距离后，可以获得较小者min。此时不能直接返回这个较小者，因为可以存在两个点分别在左边集合和右边集合。此时处理方式为，我们已经知道了左右两个集合最小的距离，那么如果存在一个点对分别在两个点集中，则一定是在分割线两侧min距离以内。如下图所示：

min_dis

此时，我们就可以先限定一部分点。随后，考虑这些点如何求最小距离，这里利用了一个原理，如上图右侧所示，如果存在距离小于min的点对，则在一个点与之前点（y值比其大的点）比较之后，最多只用比较随后的七个点。这是由于两边点集最小距离是min，所以在一个以分割线为中心长为2*min，宽为min的区域最多存在八个点，超过八个点后的点距离绝对都打于min。利用这个原理，我们将按照y坐标排序好的点集根据左右min的限制提取出来，以每个点开始比较其后续的七个点（如果有的话）。最终确定这个区域内最短距离，而后与先前的min比较取最小值。

程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

struct points{
    int x;
    int y;
};

static points *ps;
static int count1;

bool compare1(int p1, int p2)
{
    return ps[p1].x<ps[p2].x;
}

bool compare2(int p1, int p2)
{
    return ps[p1].y>ps[p2].y;
}

int get_dis(int x, int y)
{
    return (ps[x].x - ps[y].x)*(ps[x].x - ps[y].x)+(ps[x].y - ps[y].y)*(ps[x].y - ps[y].y);
}

int get_mindis(vector<int> x_sorted, vector<int> y_sorted)
{
    int num = x_sorted.size();
    if(num==1) //集合中只有一个点时使用-1标志
    {
        return -1;
    }
    if(num<4) //集合中点数很小时，直接获取最小距离
    {
        int min = -1;
        for(int i=0;i<num-1; i++)
        {
            for(int j=i+1;j<num;j++)
            {
                count1++;
                int dis = get_dis(x_sorted[i], x_sorted[j]);
                if(min == -1 || min>dis)
                {
                    min = dis;
                }
            }
        }
        return min;
    }

    if(ps[x_sorted[0]].x == ps[x_sorted[num-1]].x) //当集合中所以点都在同一列时
    {
        int min = ps[x_sorted[0]].y - ps[x_sorted[1]].y;
        for(int i=1;i<num-1;i++)
        {
            count1++;
            int dis = (ps[x_sorted[i]].y - ps[x_sorted[i+1]].y)*(ps[x_sorted[i]].y - ps[x_sorted[i+1]].y);
            if(dis<min)
            {
                min = dis;
            }
        }
        return min;
    }

    if(ps[y_sorted[0]].y == ps[y_sorted[num-1]].y)//当集合中点都在同一行时
    {
        int min = (ps[x_sorted[1]].x - ps[x_sorted[0]].x)*(ps[x_sorted[1]].x - ps[x_sorted[0]].x);
        for(int i=1;i<num-1;i++)
        {
            count1++;
            int dis = ps[x_sorted[i+1]].x - ps[x_sorted[i]].x;
            if(dis<min)
            {
                min = dis;
            }
        }
        return min;
    }

    //分组
    vector<int> next_x_1;
    vector<int> next_y_1;
    vector<int> next_x_2;
    vector<int> next_y_2;
    int mod = num/2;
    int dev_x = ps[x_sorted[mod]].x;
    for(int i=0;i<num;i++)
    {
        count1++;
        if(ps[x_sorted[i]].x<dev_x)
        {
            next_x_1.push_back(x_sorted[i]);
        }
        else{
            next_x_2.push_back(x_sorted[i]);
        }

        if(ps[y_sorted[i]].x<dev_x)
        {
            next_y_1.push_back(y_sorted[i]);
        }
        else{
            next_y_2.push_back(y_sorted[i]);
        }
    }

    int min_dis1 = get_mindis(next_x_1, next_y_2);
    int min_dis2 = get_mindis(next_x_1, next_y_2);
    int min_dis;
    if(min_dis1 == -1 || min_dis2 == -1) // 只可能有一个是-1
    {
        min_dis = min_dis1 > min_dis2 ? min_dis1 : min_dis2;
    }
    else{
        min_dis = min_dis1 < min_dis2 ? min_dis1 : min_dis2;
    }
    vector<int> merge;
    for(int i=0;i<num; i++)
    {
        count1++;
        if((ps[y_sorted[i]].x - dev_x)*(ps[y_sorted[i]].x - dev_x)<min_dis)
        {
            merge.push_back(y_sorted[i]);
        }
    }
    int mnum = merge.size();
    for(int i=0;i<mnum;i++)
    {
        for(int j=i+1; j<mnum && j<i+8;j++)
        {
            count1++;
            int dis = get_dis(merge[i], merge[j]);
            if(dis<min_dis)
            {
                min_dis = dis;
            }
        }
    }
    return min_dis;
}

int main()
{
    count1 = 0;
    int n;
    cin>>n;
    ps = new points [n];
    vector<int> x_sorted;
    vector<int> y_sorted;
    for(int i=0;i<n;i++)
    {
        cin>>ps[i].x>>ps[i].y;
        y_sorted.push_back(i);
        x_sorted.push_back(i);
    }
    sort(y_sorted.begin(), y_sorted.end(), compare2);
    sort(x_sorted.begin(), x_sorted.end(), compare1);
    int dis = get_mindis(x_sorted, y_sorted);
    cout<<"min1 dis^2 is: "<<dis<<endl;
    cout<<"count1 = "<<count1<<endl;
    
    int min = -1;

    for(int i=0;i<n;i++)
    {
        for(int j=i+1;j<n;j++)
        {
            int dis = get_dis(i, j);
            if(min == -1 && dis<min)
            {
                min =dis;
            }
        }
    }
    cout<<"min2 dis^2 is: "<<dis<<endl;
    return 0;
}

取100个点，程序执行结果为：

1
2
3
min1 dis^2 is: 117
count1 = 1095
min2 dis^2 is: 117

程序执行正确，且计算复杂度确实大幅降低，达到O(nlog(n))量级。